前言

刷题的时候又遇到全错排问题, 本来是一个很熟悉动态规划问题, 不过我按照模糊的记忆来写状态转移方程的时候发现写错了, 于是决定搜搜看相关的公式详解, 配合着理解来巩固记忆.

不过翻了几篇文章, 都是几乎一样的解释, 而且我都不是很能理解, 感觉没有解释清楚情况数如何避免重叠和不遗漏的问题.

于是写一篇我的理解, 希望能够帮助到你.

dp状态转移方程

首先, 先放上经典的公式:

dp[n]=(n-1)*(dp[n-1]+dp[n-2])

分步骤理解

首先我们考虑一个长为n的有序排列:

1, 2, 3, ..., n-1, n

其中假设前n-1中有一个数为k:

1, 2, 3, ..., k, ..., n-1, n

1. 我们取出这个k, 共有(n-1)种情况, 用[]表示空位置

1, 2, 3, ..., [], ..., n-1, n

2. 然后将k放在n的位置上, 将n拿在手里

1, 2, 3, ..., [], ..., n-1, k

3. 然后手里的n能够放在哪里, 有两种情况:

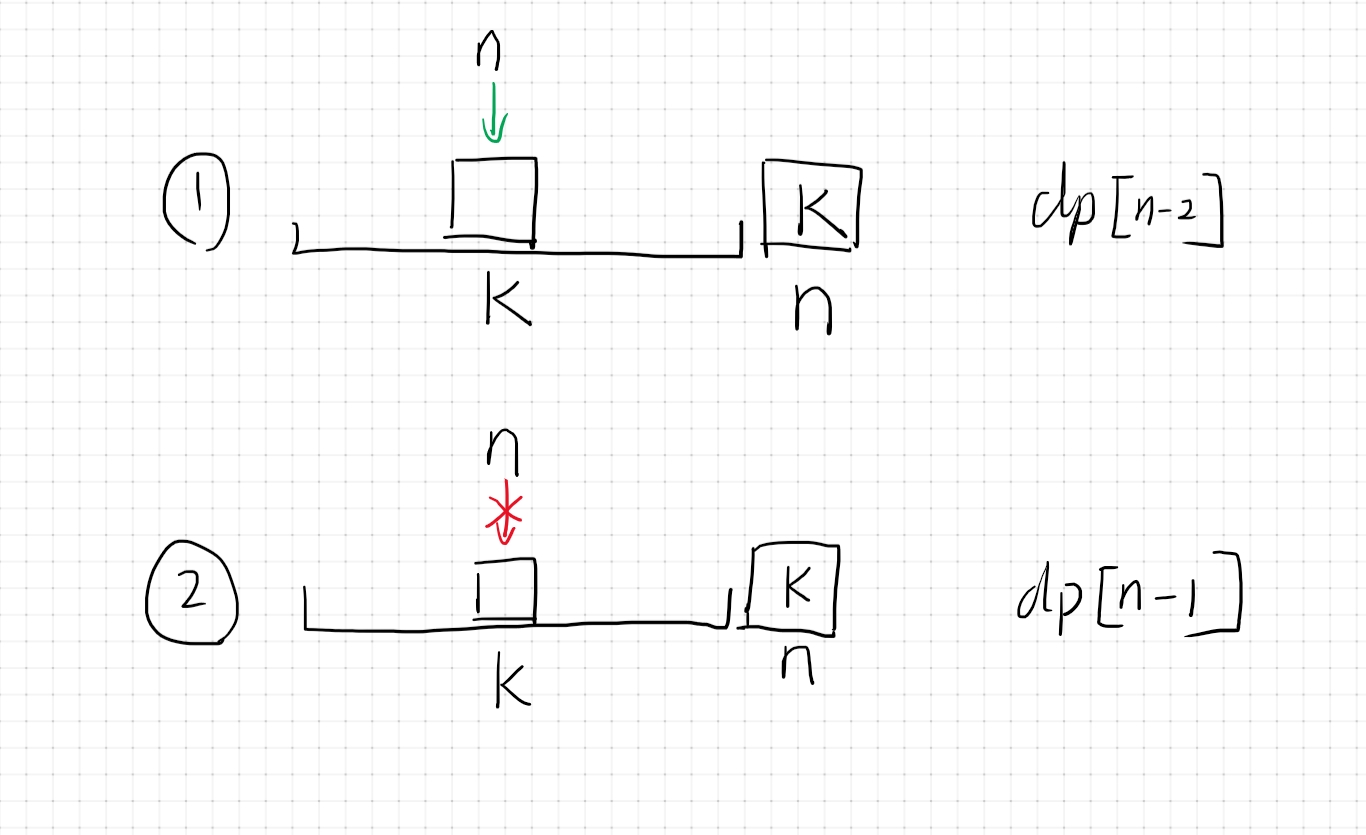
   1. n放在原本k的位置上, 即

      1, 2, 3, ..., n, ..., n-1, k
      

      这样这个序列已经固定了n和k的位置, 剩下n-2个数要全错位, 即dp[n-2]种情况.

   2. n不放在原本k的位置, 这个问题可以转变为前n-1个数全错排(因为n不能放在原本k的位置, 就相当于把n看作k), 这时候的情况数就是dp[n-1]个.

不会遗漏: 我们将前n-1个数中取k都考虑到, 然后k固定在了n的位置上, 最后能否将n放在原本k的位置上也考虑到, 所以不会遗漏.

不会重叠: n的位置只有两种情况, 放在k的位置上, 或者不放在k的位置上, 这两种情况相互独立, 不会重叠.

所以总的情况数就是: dp[n]=(n-1)*(dp[n-1]+dp[n-2])

得证.

最后符一张便于记忆的图片: